- Kepler Orbit Equation
- Kepler Orbital Speed
- Kepler Orbital Period Equation
- Kepler Orbit Element
- Kepler Orbit Period
- Kepler Orbit Laws
- Kepler Orbit Calculator
By Dan Hooper Ph.D., University of Chicago
Johannes Kepler was one of the leading characters in the history of astronomy. His most famous achievement was the three laws of planetary motion, still taught in courses today. However, like all other human beings, he was not perfect and made mistakes. Were his three laws right at all?
Johannes Kepler was one of the most influential figures in the history of astronomy. His three laws of planetary movement changed the world of science significantly and became a foundation for other scientists to build theories upon. Nonetheless, there are theories in his past that are not even close to reality. To know what he got wrong, one must first understand what he got right.
The Three Laws of Planetary Motion
Kepler's Three Laws can be used to describe the motion of the Planets: Planets move in orbits that are ellipses The planets move such that the line between the Sun and the Planet sweeps out the same area in the same area in the same time no matter where in the orbit. Kepler’s third law states that the square of the period is proportional to the cube of the semi-major axis of the orbit. In Satellite Orbits and Energy, we derived Kepler’s third law for the special case of a circular orbit. Kepler Orbits ¶ Skyfield now offers basic support for computing the position of a comet or minor planet whose elliptical, parabolic, or hyperbolic orbit is provided as Kepler orbital elements.
In 1609, Kepler published a book containing the first two laws. The book also revealed his new model of the solar system, which was against what most scientists back then believed. He stated that planets moved in elliptical orbits through the solar system, with the Sun located at one focus of the ellipse. Before Kepler, they believed that all orbits in the solar system were perfectly circular.
The first law is concerned with the route that a given planet will take around the Sun. The second one focuses on the speed of the orbiting object against its distance from the Sun: the closer the planet gets to the Sun in its orbit, the faster it moves.
About ten years later, Kepler added his third law: that square of the orbital period divided by the cube of orbit’s semi-major axis is the same for all planets. Although not immediately accepted, his three laws took science to the next level. Why was he initially not appreciated?
This is a transcript from the video series What Einstein Got Wrong.Watch it now, on The Great Courses Plus.
Kepler’s Family Background
Johannes Kepler’s father was a mercenary who left the family when Kepler was five. His mother was accused of practicing witchcraft, as she was an herbalist and a healer. Kepler attended school as much as he could, and his talent took him to university to become a Lutheran minister.
He studied theology and philosophy, alongside mathematics and astronomy. After graduation, he began teaching mathematics and astronomy in a Protestant school in Graz, Austria. There, he got the idea which was very wrong, but revolutionary to science.
Learn more about cosmology and the cosmological constant.
How Kepler Got His Revolutionary Theory
In 1595, as Kepler was teaching geometry, his mind flew off in a different direction. It started with a circle and an equilateral triangle located around the circle in a way that each side of the triangle barely touched the circle. Next, another circle would surround the triangle, such that all three vertices of the triangle touch the edge of the outer circle. Geometrically, the bigger circle is twice the small one—a 2:1 ratio.
Kepler applied this to the planets and stated that the solar system was built upon geometrical objects called Platonic solids that are a specific type of three-dimensional shape. They have identical sides or surfaces, edges of equal length, and angles of equal extent.
The most famous examples of Platonic solids are a tetrahedron—a four-sided shape with an equilateral triangle on each side—and a six-sided cube. There are five possible Platonic solids with four, six, eight, twelve, and twenty sides.
Kepler’s Model of the Solar System
The model Kepler presented was based on a sequence of six spheres and the five Platonic solids, each located between two spheres. Back then, only six planets were discovered as Uranus and Neptune’s discovery took until the 18th and 19th centuries. Thus, each sphere represented one planet.
Initially, it seemed to explain the approximate ratios of the orbits of the six planets. It also gave a reason why there are only six planets—because there are only five Platonic shapes, each of which needs to fit between the orbit of two planets, only once. Kepler published this theory in detail, in his book Mysterium Cosmographicum. Despite all the value he gave to this theory, we now know how wrong it was.
Kepler cherished the theory as his most significant work, long after he had discovered the three laws. However, the number of planets in the solar system or any other system in the universe is not predictable. Many of the numbers appearing everywhere are out of a mere accident, just like the number of planets.
Kepler thought his greatest achievement was the wrong solar system he drew, but it was the three laws that were so right to survive to date.
Kepler Orbit Equation
Learn more about the cosmological constant and dark energy.
Common Questions about Johannes Kepler
Q: What impact did Johannes Kepler have?Johannes Kepler was a cornerstone of the science of astronomy. His three laws of planetary motion, discovered over decades, are the foundation of many scientific findings in the same area. Even Isaac Newton used Kepler’s laws to build his theories, and they are still taught at physics and astronomy introductory courses.
Q: What did Johannes Kepler believe about the universe?Before he discovered the three laws of planetary motion, Johannes Kepler proposed a model of the solar system, with almost nothing accurate in it. The model described the solar system as a sequence of alternating spheres and Platonic solids, which is far away from reality.
Q: What is Johannes Kepler famous for?Johannes Kepler is the scientist who discovered the three critical laws of planetary motion throughout his scientific life.
Keep Reading
Order in Randomness: Fractals and Chaotic Systems
Unstable Systems: The Three-Body Problem and the Butterfly Effect
Understanding the Universe: From Probability to Quantum Theory
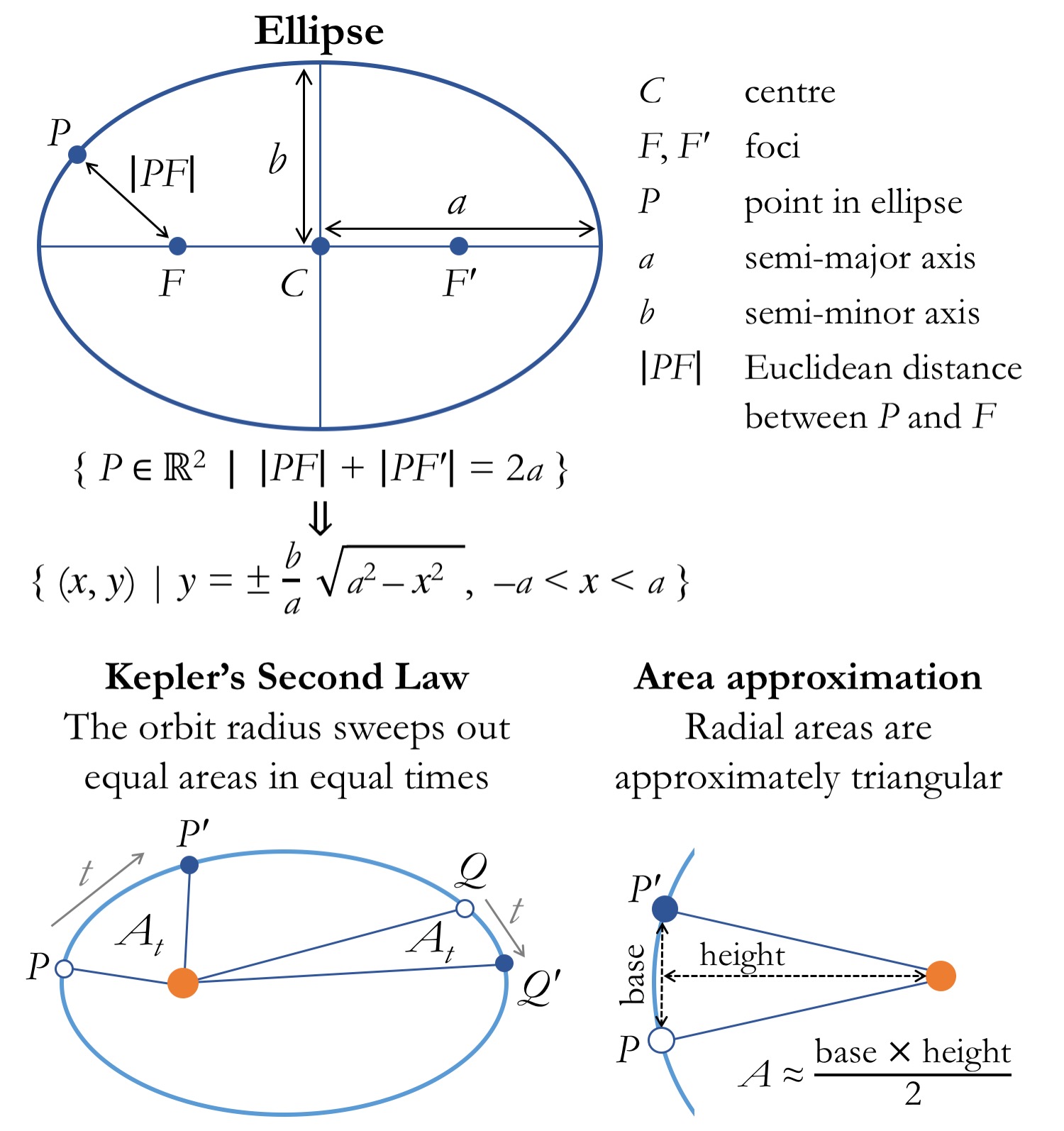
Next:Model of Hipparchus Up:Geometric Planetary Orbit Models Previous:IntroductionKepler's geometric model of a heliocentric planetary orbit is summed up in his three well-known laws of planetary motion.According to Kepler's first law, all planetary orbits are ellipses which are confocal with the sun and lie in afixed plane.Moreover, according to Kepler's second law, the radius vector which connects the sun to a given planet sweeps out equal areas in equal time intervals.
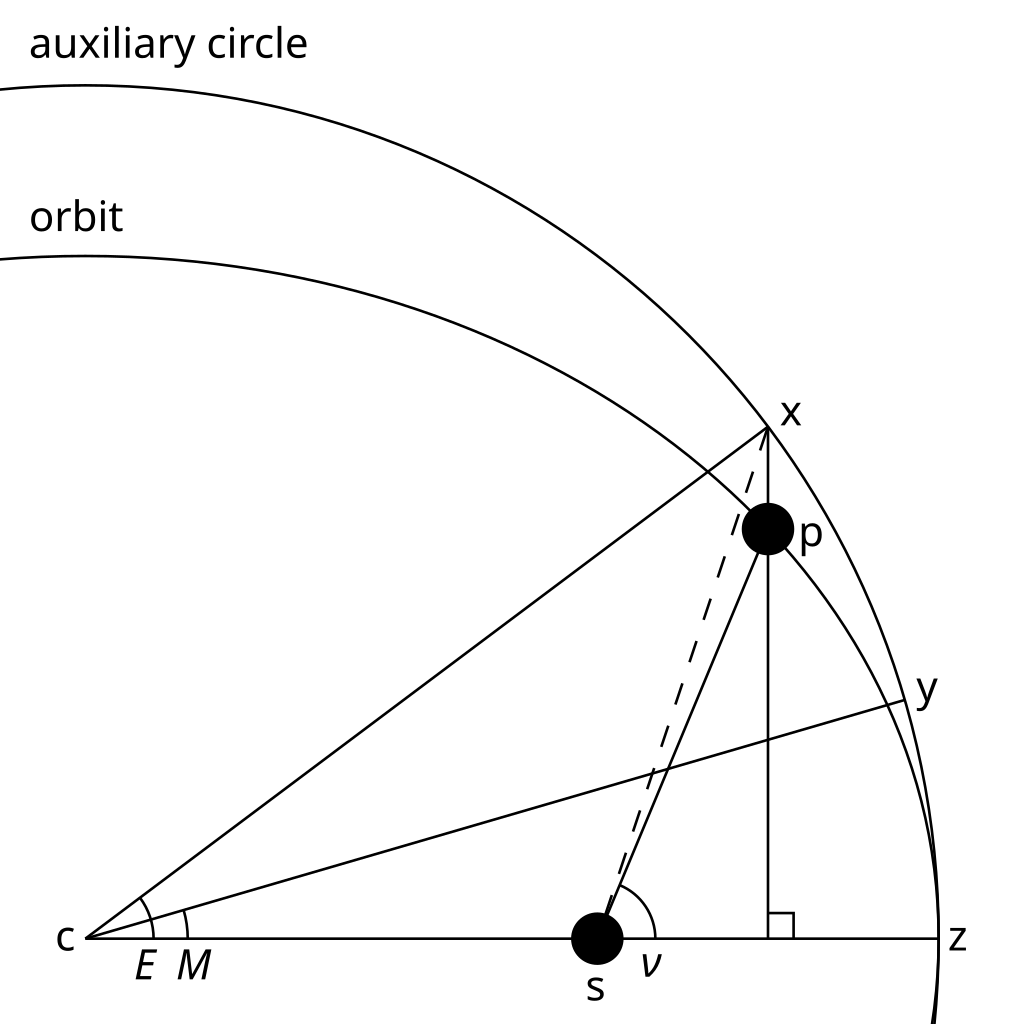
Consider Figure 17. is half of an elliptical planetary orbit. Furthermore, is thegeometric center of the orbit, the focus at which the sun is located, the instantaneous position of the planet, the perihelion point (i.e., the planet's point of closest approach to the sun),and the aphelion point (i.e., the point of furthest distance from the sun). The ellipse is symmetric about, which is termed the major axis, and about ,which is termed the minor axis.The length is called the orbitalmajor radius. The length represents the displacement of the sun fromthe geometric center of the orbit, and is generally written , where is termed theorbital eccentricity, where . The length is calledthe orbital minor radius. The length represents the radial distance of the planet from the sun.Finally, the angle is the angular bearing of the planet from the sun,relative to the major axis of the orbit, and is termed the true anomaly.
is half of a circle whose geometric center is , and whoseradius is . Hence, the circle passes through the perihelion and aphelionpoints. is the point at which the perpendicular from meets the major axis . The point where producedmeets circle is denoted . Finally,the angle is called the elliptic anomaly.
Now, the equation of the ellipse is
| (60) |
 where and are the perpendicular distances from the minor and majoraxes, respectively. Likewise, the equation of the circle is
where and are the perpendicular distances from the minor and majoraxes, respectively. Likewise, the equation of the circle isHence, if then
| (62) |
and it follows that
Now, . Furthermore, it is easily demonstrated that , , , and . Consequently, Eq. (63) yields
| (64) |
Also, since , we have
Taking the square root of the sum of the squares of the previous two equations, we obtain
Kepler Orbital Speed
| (66) |
which can be combined with Eq. (65) to give
Now, according to Kepler's second law,
| (68) |
where is the time at which the planet passes point , the time at which it passes the perihelion point,and the orbital period
 .However,
.However,But,

| (70) |
since for all values of . In addition,
Hence, we can write
| (72) |
According to Eqs. (64) and (65), , and , sothe above expression reduces to
where
| (74) |
is an angle which is zero at the perihelion point, increases uniformly in time, and has a repetition period whichmatches the period of the planetary orbit. This angle is termed the mean anomaly.
In summary, the radial and angular polar coordinates, and , respectively,of a planet in a Keplerian orbit about the sun are specified as implicit functionsof the mean anomaly, which is a linear function of time, by thefollowing three equations:
It turns out that the earth and the five visible planets all possess low eccentricity orbits characterized by . Hence, it is a good approximation to expand the above three equationsusing as a small parameter. To second-order, weget
| (78) |
| (79) |
| (80) |
Kepler Orbital Period Equation
Kepler Orbit Element
Finally, these equations can be combined to give and as explicit functions of themean anomaly:Next:Model of Hipparchus
Kepler Orbit Period
Up:Kepler Orbit Laws
Geometric Planetary Orbit ModelsKepler Orbit Calculator
Previous:IntroductionRichard Fitzpatrick2010-07-21